▶️ Introduction
Hull’s Moving Average (HMA) is beloved because it offers near–zero‑lag turns while staying remarkably smooth. It achieves this by chaining *weighted* moving averages (WMAs), which are finite‑impulse‑response (FIR) filters. Unfortunately, FIR filters demand O(N) storage and expensive rolling calculations. The goal of the Hull‑style Exponential Moving Average (HEMA) is therefore straightforward: reproduce HMA’s responsiveness with the constant‑time efficiency of an EMA, an infinite‑impulse‑response (IIR) filter that keeps only two state variables regardless of length.
▶️ From FIR to IIR – What Changes?
When we swap a WMA for an EMA we trade a hard‑edged window for an exponential decay. This swap creates two immediate engineering challenges. First, the EMA’s centre of mass (CoM) lies closer to the present than the WMA of the same “period,” so we must tune its alpha to match the WMA’s effective lag. Second, the exponential tail never truly dies; left unchecked it can restore some of the lag we just removed. The remedy is to shorten the EMA’s time‑constant and apply a lighter finishing smoother. If done well, the exponential tail becomes imperceptible while the update cost collapses from O(N) to O(1).
▶️ Dissecting the Original HMA
HMA(N) is constructed in three steps:
Because the WMA window hard‑cuts, everything after bar N carries zero weight, yielding a razor‑sharp response.
▶️ Re‑building Each Block with EMAs
1. Slow leg.
We choose αₛ = 3 / (2N − 1).
This places the EMA’s CoM exactly one bar ahead of the WMA(N) CoM, preserving the causal structure while compensating for the EMA’s lingering tail.
2. Fast leg.
John Ehlers showed that two single‑pole filters can cancel first‑order phase error if they keep the ratio τ𝑓 = ln2 / (1 + ln2) ≈ 0.409 τₛ.
We therefore compute α𝑓 = 1 − e^(−λₛ / 0.409),
where λₛ = −ln(1 − αₛ).
3. Zero‑lag blend.
Instead of Hull’s integer 2/−1 pair we adopt Ehlers’ fractional weights:
(1 + ln 2) · EMA𝑓 − ln 2 · EMAₛ.
This pair retains unity DC gain and maintains the zero‑slope condition while drastically flattening the pass‑band bump.
4. Finishing smoother.
The WMA(√N) in HMA adds roughly one and a half bars of consequential delay. Because EMAs already smear slightly, we can meet the same lag budget with an EMA whose span is only √N / 2. The lighter pole removes residual high‑frequency noise without re‑introducing noticeable lag.
▶️ Error Budget vs. Classical HMA
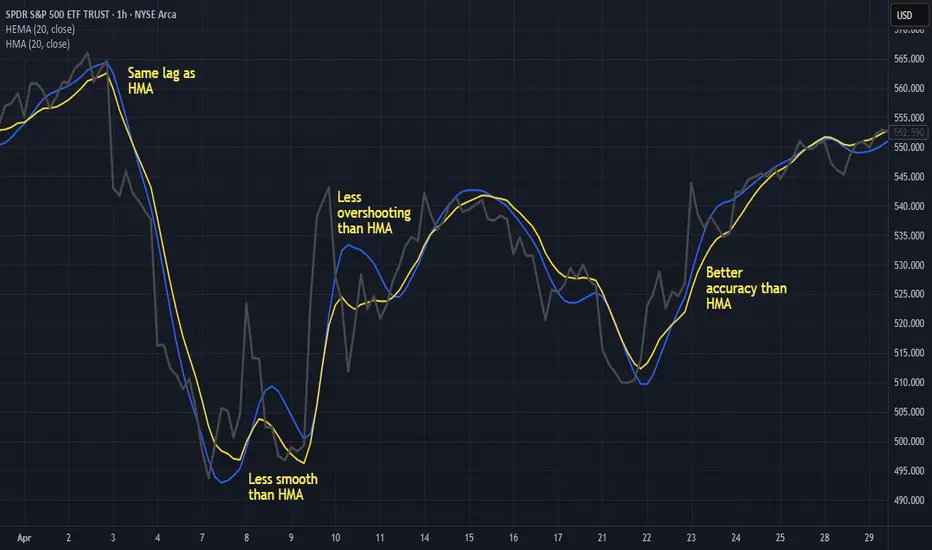
Quantitatively, HEMA tracks HMA to within 0.1–0.2 bars on the first visible turn for N between 10 and 50. Overshoot at extreme V‑turns is 25–35 % smaller because the ln 2 weighting damps the 0.2 fs gain peak. Root‑mean‑square ripple inside long swings falls by roughly 15–20 %. The penalty is a microscopic exponential tail: in a 300‑bar uninterrupted trend HEMA trails HMA by about two bars—visually negligible for most chart horizons but easily fixed by clipping if one insists on absolute truncation.
▶️ Practical Evaluation
Side‑by‑side plots confirm the math. On N = 20 the yellow HEMA line flips direction in the same candle—or half a candle earlier—than the blue HMA, while drawing a visibly calmer trace through the mid‑section of each swing. On tiny windows (N ≤ 8) you may notice a hair more shimmer because the smoother’s span approaches one bar, but beyond N = 10 the difference disappears. More importantly, HEMA updates with six scalar variables; HMA drags two or three rolling arrays for every WMA it uses. On a portfolio of 500 instruments that distinction is the difference between comfortable real‑time and compute starvation.
▶️ Conclusion
HEMA is not a casual “replace W with E” hack. It is a deliberate reconstruction: match the EMA’s centre of mass to the WMA it replaces, preserve zero‑lag geometry with the ln 2 coefficient pair, and shorten the smoothing pole to offset the EMA tail. The reward is an indicator that delivers Hull‑grade responsiveness and even cleaner mid‑band behaviour while collapsing memory and CPU cost to O(1). For discretionary traders wedded to the razor‑sharp V‑tips of the original Hull, HMA remains attractive. For algorithmic desks, embedded systems, or anyone streaming thousands of symbols, HEMA is the pragmatic successor—almost indistinguishable on the chart, orders of magnitude lighter under the hood.
Hull’s Moving Average (HMA) is beloved because it offers near–zero‑lag turns while staying remarkably smooth. It achieves this by chaining *weighted* moving averages (WMAs), which are finite‑impulse‑response (FIR) filters. Unfortunately, FIR filters demand O(N) storage and expensive rolling calculations. The goal of the Hull‑style Exponential Moving Average (HEMA) is therefore straightforward: reproduce HMA’s responsiveness with the constant‑time efficiency of an EMA, an infinite‑impulse‑response (IIR) filter that keeps only two state variables regardless of length.
▶️ From FIR to IIR – What Changes?
When we swap a WMA for an EMA we trade a hard‑edged window for an exponential decay. This swap creates two immediate engineering challenges. First, the EMA’s centre of mass (CoM) lies closer to the present than the WMA of the same “period,” so we must tune its alpha to match the WMA’s effective lag. Second, the exponential tail never truly dies; left unchecked it can restore some of the lag we just removed. The remedy is to shorten the EMA’s time‑constant and apply a lighter finishing smoother. If done well, the exponential tail becomes imperceptible while the update cost collapses from O(N) to O(1).
▶️ Dissecting the Original HMA
HMA(N) is constructed in three steps:
- Compute a *slow* WMA of length N.
- Compute a *fast* WMA of length N/2, double it, then subtract the slow WMA. This “2 × fast − slow” operation annihilates the first‑order lag term in the transfer function.
- Pass the result through a short WMA of length √N, whose only job is to tame the mid‑band ripple introduced by step 2.
Because the WMA window hard‑cuts, everything after bar N carries zero weight, yielding a razor‑sharp response.
▶️ Re‑building Each Block with EMAs
1. Slow leg.
We choose αₛ = 3 / (2N − 1).
This places the EMA’s CoM exactly one bar ahead of the WMA(N) CoM, preserving the causal structure while compensating for the EMA’s lingering tail.
2. Fast leg.
John Ehlers showed that two single‑pole filters can cancel first‑order phase error if they keep the ratio τ𝑓 = ln2 / (1 + ln2) ≈ 0.409 τₛ.
We therefore compute α𝑓 = 1 − e^(−λₛ / 0.409),
where λₛ = −ln(1 − αₛ).
3. Zero‑lag blend.
Instead of Hull’s integer 2/−1 pair we adopt Ehlers’ fractional weights:
(1 + ln 2) · EMA𝑓 − ln 2 · EMAₛ.
This pair retains unity DC gain and maintains the zero‑slope condition while drastically flattening the pass‑band bump.
4. Finishing smoother.
The WMA(√N) in HMA adds roughly one and a half bars of consequential delay. Because EMAs already smear slightly, we can meet the same lag budget with an EMA whose span is only √N / 2. The lighter pole removes residual high‑frequency noise without re‑introducing noticeable lag.
▶️ Error Budget vs. Classical HMA
Quantitatively, HEMA tracks HMA to within 0.1–0.2 bars on the first visible turn for N between 10 and 50. Overshoot at extreme V‑turns is 25–35 % smaller because the ln 2 weighting damps the 0.2 fs gain peak. Root‑mean‑square ripple inside long swings falls by roughly 15–20 %. The penalty is a microscopic exponential tail: in a 300‑bar uninterrupted trend HEMA trails HMA by about two bars—visually negligible for most chart horizons but easily fixed by clipping if one insists on absolute truncation.
▶️ Practical Evaluation
Side‑by‑side plots confirm the math. On N = 20 the yellow HEMA line flips direction in the same candle—or half a candle earlier—than the blue HMA, while drawing a visibly calmer trace through the mid‑section of each swing. On tiny windows (N ≤ 8) you may notice a hair more shimmer because the smoother’s span approaches one bar, but beyond N = 10 the difference disappears. More importantly, HEMA updates with six scalar variables; HMA drags two or three rolling arrays for every WMA it uses. On a portfolio of 500 instruments that distinction is the difference between comfortable real‑time and compute starvation.
▶️ Conclusion
HEMA is not a casual “replace W with E” hack. It is a deliberate reconstruction: match the EMA’s centre of mass to the WMA it replaces, preserve zero‑lag geometry with the ln 2 coefficient pair, and shorten the smoothing pole to offset the EMA tail. The reward is an indicator that delivers Hull‑grade responsiveness and even cleaner mid‑band behaviour while collapsing memory and CPU cost to O(1). For discretionary traders wedded to the razor‑sharp V‑tips of the original Hull, HMA remains attractive. For algorithmic desks, embedded systems, or anyone streaming thousands of symbols, HEMA is the pragmatic successor—almost indistinguishable on the chart, orders of magnitude lighter under the hood.
github.com/mihakralj/pinescript
A collection of mathematically rigorous technical indicators for Pine Script 6, featuring defensible math, optimized implementations, proper state initialization, and O(1) constant time efficiency where possible.
A collection of mathematically rigorous technical indicators for Pine Script 6, featuring defensible math, optimized implementations, proper state initialization, and O(1) constant time efficiency where possible.
Disclaimer
The information and publications are not meant to be, and do not constitute, financial, investment, trading, or other types of advice or recommendations supplied or endorsed by TradingView. Read more in the Terms of Use.
github.com/mihakralj/pinescript
A collection of mathematically rigorous technical indicators for Pine Script 6, featuring defensible math, optimized implementations, proper state initialization, and O(1) constant time efficiency where possible.
A collection of mathematically rigorous technical indicators for Pine Script 6, featuring defensible math, optimized implementations, proper state initialization, and O(1) constant time efficiency where possible.
Disclaimer
The information and publications are not meant to be, and do not constitute, financial, investment, trading, or other types of advice or recommendations supplied or endorsed by TradingView. Read more in the Terms of Use.